こんにちは!お小遣いを競馬で稼ぐサラリーマン改め
オッズマーケターのチョコぱんです。
さて本日は2020年10月18日(日)京都第11レースで行われる
第25回秋華賞を過去データから注目馬を予想したいと思います!
特に今回の秋華賞ですが、ひょっとすると史上初の無敗の3冠牝馬デアリングタクトが誕生するかもしれないのでデアリングタクトを信用していいのかどうかもチェックしていきます。
秋華賞は京都内回り2000m!有利な条件となる馬は?
2020年の秋華賞は京都競馬場内回りの芝2000mで行われます。
この京都競馬場の内回り、2000mというのが秋華賞を当てる上で欠かせないポイントですね。
京都内周り2000mだと直線が短く、逃げ馬が圧倒的有利で差し、追い込み馬は脚を余してしまう事も多々あります。
なのでデアリングタクトにはちょっと不利な条件かもしれません。
そういった事も踏まえて過去10年における秋華賞のデータを調べていきます。
秋華賞に強い種牡馬

秋華賞の種牡馬実績では単勝回収率はともかく、ディープインパクト産駒が過去10年で4勝、2着も4回と素晴らしい実績を残しています。
出走頭数もそれなりに多いのですが京都競馬場はディープのお庭なので馬券候補からは外せないでしょう。
まず第一候補としてはディープインパクト産駒は抑えておく必要があります。
今回の秋華賞でのディープインパクト産駒は
- 1枠1番ミヤマザクラ
- 1枠2番リアアメリア
- 4枠8番ソフトフルート
- 5枠9番サンクテュエール
- 6枠12番マジックキャッスル
- 7枠14番オーマイダーリン
と18頭中6頭もいます!3分の1で出走するので今回もディープ産駒が馬券内に来ても全く不思議ではありません。
でもできれば人気薄が来てくれれば(笑)
現状で馬券のうまみがありそうなのは
- ソフトフルート
- オーマイダーリン
が実力の割には不当に人気が低そうで狙い目かもしれません。
秋華賞に強い騎手
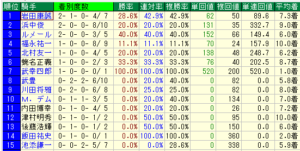
過去10年における秋華賞データでは2勝している騎手が3名いますね。
- 岩田康誠
- 浜中俊
- ルメール
やはり相性がよさそうな3名の騎手は頭に入れておくべきかもしれません。
しかも今回の秋華賞においては唯一、ルメールのみ騎乗なので狙ってよさそうですよ!
ちなみにルメール騎乗馬は
ディープインパクト産駒のサンクテュエール!
ルメール×藤沢和雄調教師の強力タッグがデアリングタクトの牙城を崩すかもしれません。
そのデアリングタクト騎乗の主戦騎手、松山弘平ですが
過去の秋華賞では5回騎乗してなんと5回とも着外という結果でした!
松山ジョッキーにとっては鬼門の秋華賞ですが
そこは最強牝馬になりえる素質があるデアリングタクトなので過去は無視してもいいでしょう。
当然秋華賞では優勝候補である事には変わりがありません。
秋華賞での人気別信頼度
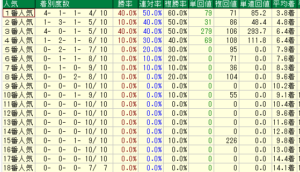
秋華賞での人気別信頼度ですが
- 1番人気
- 3番人気
がいずれも過去10年で4勝と実績を残しています。
そして狙い目は3番人気ですね!
単勝回収値も279円で高い数値を残していますので3番人気は外せないでしょう。
ちなみに執筆時での秋華賞3番人気は
3枠5番ウインマイティーとなっています。ウインマイティーはオークスでは13番人気ながら3着に入っていますし、うまく内枠を引けたのでひょっとするかも?
まとめ
今回は2020年秋華賞の過去データから注目馬を紹介しました。
データ的にはデアリングタクトは厳しそうですが、
馬券としてはデアリングタクトから注目馬3頭くらいに絞っての馬券で勝負するのがいいかもしれません。
いずれにせよ、空前の無敗の3冠牝馬誕生が目の前で見られるのはすごい事ですよ!
今回は以上となります。最後までお読みいただきありがとうございました。
今なら、無料登録で【馬王Z】自動運転攻略法を提供!!
競馬予想なら!
競馬最強の法則WEB
![]()

















コメントを残す